ASSP first identifies the continuous stretches in the protein structure and then classifies these structures into different SSEs (mainly helices) based on the cutoff values of different local geometrical parameters. In order to determine the cutoff values, we considered helices or part of helices, which were commonly assigned by DSSP and STRIDE. Total of 46, 5465 and 2340 π, α and 310 helices were found respectively. The starting (N1) and ending (C1) residue of each helix were assumed to be a part of helix. We extended each helix at both terminii by one residue (Ncap and Ccap). Hence, the repeating unit (step) involving the Cα atom of Ncap or Ccap will also contribute in defining the helix terminii.
Cutoff values of different structural parameters for different helices:
Right handed helices:
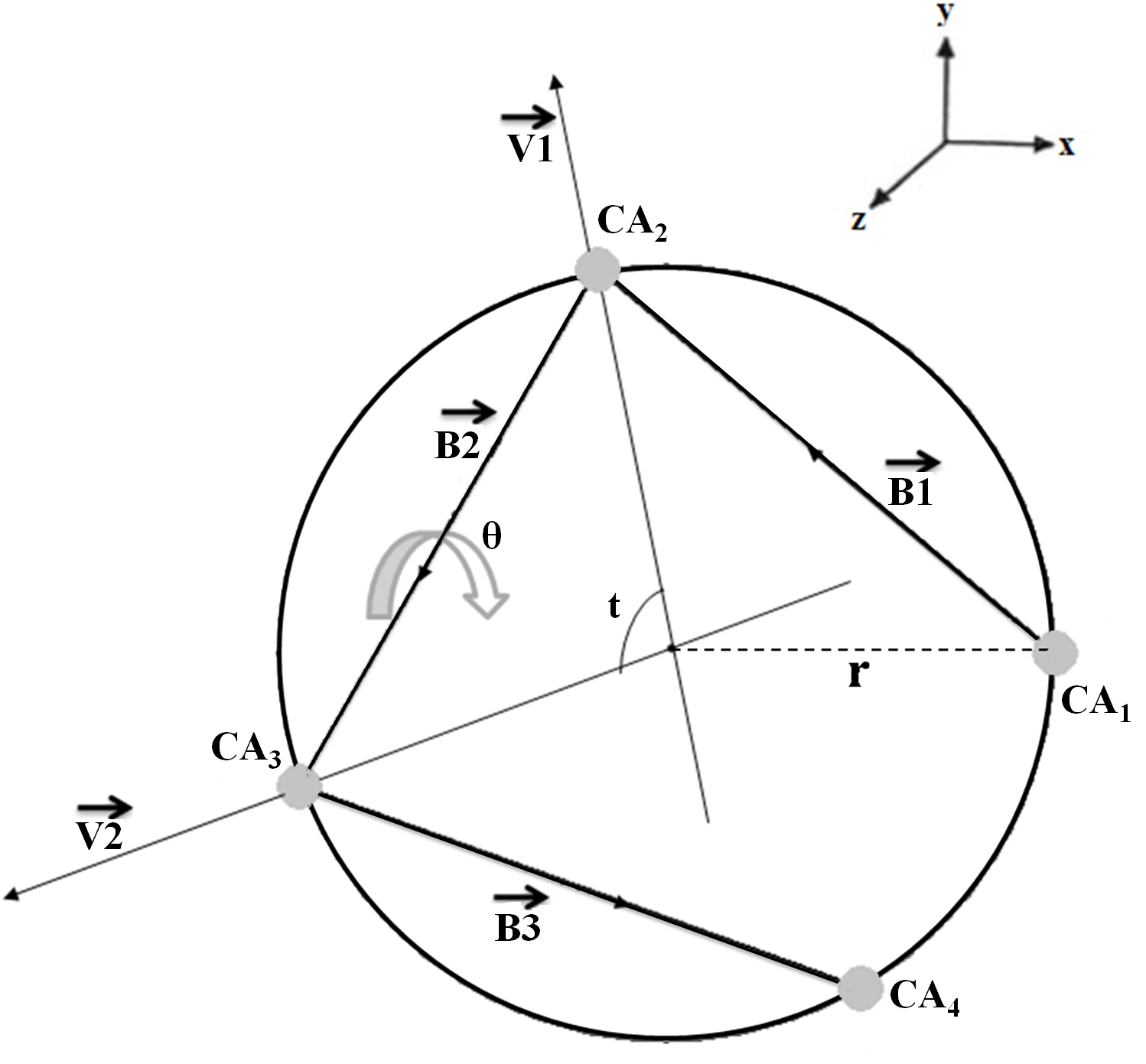
Right handed π, α and 310 helices fall into this category. Steps with all the residues belonging to the helices were considered. All the steps were checked for the continuity and not selected, if they do not found to satisfy the continuity criteria. Total number of steps and number of steps after removing the discontinuous ones are tabulated below:
| Serial Number | Helix Type | Number of Steps | Steps after modification |
|---|---|---|---|
| 1. | π | 199 | 132 |
| 2. | α | 62303 | 61543 |
| 3. | 310 | 5498 | 5037 |
Mean and Standard deviation of the geometrical parameters for each type of helices are defined using the parameters of steps after modification.
Left handed helices:Left handed π, α and 310 helices fall into this category. Individual cutoff values of corresponding right handed helices were used, except the twist value. Twist is modified by subtracting it from 360°.
PolyProline II helices:
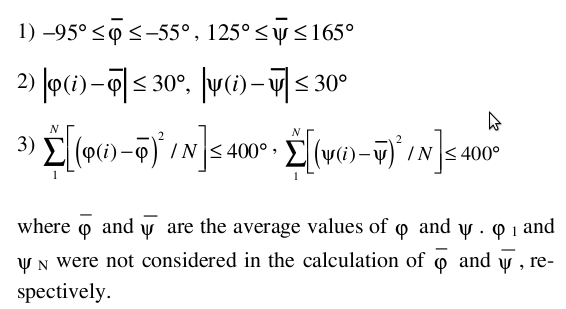
All the continuous stretches with 2 or more than 2 steps and residues satisfying the above criteria, were selected. Total number was found to be 254. Out of 254 continuous stretches, 123 were found to be a part of Strand according to Stride or DSSP and hence not considered for the calculation of the lower and upper limit of the geometric parameters for PPII helices.
Mean (Std.) and Median for various helices. Since the distributions follow normal distribution, (Mean ± Std) used as upper and lower limit for each parameters of different helices.
| π | α | 310 | PPII | |||||
|---|---|---|---|---|---|---|---|---|
| Parameters | Mean (Std.) | Median | Mean (Std.) | Median | Mean (Std.) | Median | Mean (Std.) | Median |
| Twist (˚) | 85.9 (8.0) | 83.7 | 98.7 (4.9) | 98.6 | 109.1 (5.8) | 109.5 | 238.8 (15.2) | 239.1 |
| Rise per Residue (Å) | 1.2 (0.3) | 1.2 | 1.5 (0.2) | 1.5 | 1.9 (0.2) | 1.8 | 3.0 (0.2) | 3.0 |
| Vtor (˚) | 32.1 (10.5) | 32 | 50.0 (9.1) | 49.8 | 69.4 (7.5) | 67.5 | 250.7 (19.5) | 250.8 |
| Radius (Å) | 2.7 (0.3) | 2.7 | 2.3 (0.1) | 2.3 | 2.1 (0.1) | 2.1 | 1.5 (0.4) | 1.6 |